Introduction:
A groundbreaking development has emerged in the realm of mathematics with the introduction of AlphaGeometry, an artificial intelligence program crafted by a team led by Trieu H. Trinh from Google DeepMind and New York University. This advanced AI has demonstrated its proficiency in tackling challenging geometry problems from the International Mathematical Olympiad (IMO), as disclosed in a recent publication in the journal Nature. The success of AlphaGeometry suggests a significant shift in the convergence of artificial intelligence and the resolution of intricate mathematical problems.
The Challenge:
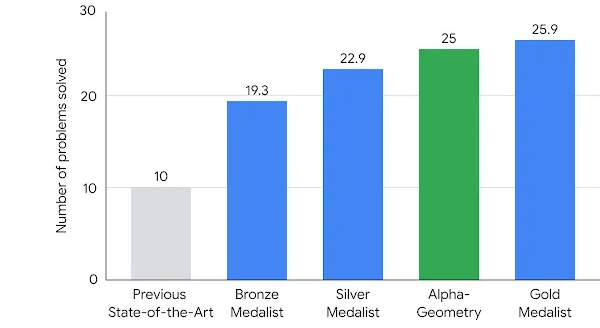
The International Mathematical Olympiad is widely acknowledged for presenting demanding problems to the brightest pre-university minds globally. In a significant development, AI programs appear prepared to join the ranks of these accomplished problem solvers. AlphaGeometry’s capacity to successfully address 25 out of 30 geometry problems from past IMOs positions it alongside the top human participants who have achieved gold medals.
AI’s Struggle in Mathematical Problem Solving:
Traditionally, AI programs, including large language models like GPT-4, confronted difficulties when addressing complex mathematical problems. The limitations stemmed from inadequate access to relevant data and the intricate task of translating human-generated proofs into formal programming languages. The domain of geometry, recognized for its intricate proofs and distinctive challenges, emerged as a particularly formidable area for AI.
The AlphaGeometry Approach:
Trinh and his team introduced a unique approach to tackle these issues. Instead of relying on formal programming languages designed for geometry, they established a dataset utilizing an algorithm that generated initial geometric “premises.” These premises, including components like triangles with illustrated heights and identified points, served as a basis for deductive algorithms to deduce additional properties.
Dataset Creation:
Utilizing a deductive algorithm, the researchers inferred additional properties of geometric objects, culminating in the development of a training dataset that included theorems and corresponding proofs. With a vast collection exceeding 100 million problems, this dataset eliminated the requirement to translate proofs generated by humans into a formal language, marking a significant breakthrough in the field.

The Missing Piece:
While deductive algorithms proved effective for simpler problems, addressing the challenges posed by IMO-level theorems required a more sophisticated approach. Trinh emphasized the need for generating new proof terms, which involves introducing fresh auxiliary elements like points and lines – a task ideally suited for an AI system similar to GPT-4.
The Implications:
AlphaGeometry’s success not only emphasizes the potential of AI in addressing mathematical problems but also initiates opportunities to explore the creative capacities of these systems. As AI progresses, its incorporation into prestigious competitions like the IMO has the potential to reshape the landscape of mathematical achievements, introducing novel perspectives and solutions to enduring problems.
Conclusion:
AlphaGeometry’s accomplishment in addressing IMO geometry challenges is indicative of the advancements in AI capabilities. The integration of deductive algorithms, inventive dataset construction, and the aptitude for generating new proof terms establishes AI as a robust participant in the domain of mathematical Olympiads. Observing this transformative moment, the future presents exciting prospects for the contribution of AI in pushing the boundaries of mathematical exploration.



